提醒:点这里加小编微信(领取免费资料、获取最新资讯、解决考教师一切疑问!)
请认真阅读下述材料,并按要求作答。
【参考设计】
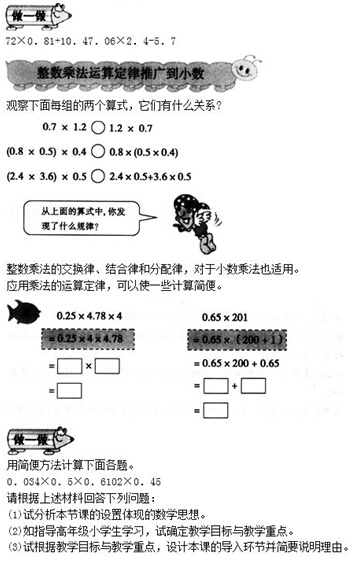
(1)本课中体现了整数乘法的交换律、分配律和结合律。其设置体现的数学思想为类比思想。类比思想是指依据两类数学对象的相似性,有可能将已知的一类数学对象的性质迁移到另一类数学对象上去的思想。比如加法交换律、乘法交换律、长方形的面积公式、平行四边形面积公式和三角形面积公式等。
类比思想不仅使数学知识容易理解,而且使公式的记忆变得自然、简洁。
(2)教学目标:
①知识与技能目标:了解小数混合运算顺序与整数混合运算顺序是一致的,有效掌握小数混合运算的运算顺序。②过程与方法目标:通过自主讨论、合作学习的途径与方法,让学生感悟知识的形成过程,在体会知识产生和发展的过程中学会知识的迁移。③情感态度与价值观目标:将数学活动与学生的生活经验相结合,启发学生运用不同思路解决问题,培养学生的创新意识。
教学重点:小数混合运算的运算顺序。
(3)导入环节设计:
教师通过多媒体列出整数连乘乘加的练习。17×4×6010×15-3026×6+25
引导学生理解整数连乘的规律是从左到右依次计算。
整数连乘乘加乘减混合运算的顺序:先算乘法,再算加法或减法。
教师总结:同学们已经学会了整数的连乘、乘加、乘减混合运算,实际在生活中,不但会遇到整数的计算问题,还会有小数的计算问题,那今天我们就共同找出小数的混合运算规律。这节课我们就来为我们学校图书馆的建设出一份力。
设计理由:运用温故知新的导人方法。学生的学习是由浅入深、循序渐进的过程。通过复习学生原有知识
内容里与新知识相联系的有关内容,提出符合学生知识水平、富有启发性的问题、小测验等形式多样的教学活动作为新旧知识联系的支点,导入新课。
【参考设计】
(1)本课中体现了整数乘法的交换律、分配律和结合律。其设置体现的数学思想为类比思想。类比思想是指依据两类数学对象的相似性,有可能将已知的一类数学对象的性质迁移到另一类数学对象上去的思想。比如加法交换律、乘法交换律、长方形的面积公式、平行四边形面积公式和三角形面积公式等。
类比思想不仅使数学知识容易理解,而且使公式的记忆变得自然、简洁。
(2)教学目标:
①知识与技能目标:了解小数混合运算顺序与整数混合运算顺序是一致的,有效掌握小数混合运算的运算顺序。②过程与方法目标:通过自主讨论、合作学习的途径与方法,让学生感悟知识的形成过程,在体会知识产生和发展的过程中学会知识的迁移。③情感态度与价值观目标:将数学活动与学生的生活经验相结合,启发学生运用不同思路解决问题,培养学生的创新意识。
教学重点:小数混合运算的运算顺序。
(3)导入环节设计:
教师通过多媒体列出整数连乘乘加的练习。17×4×6010×15-3026×6+25
引导学生理解整数连乘的规律是从左到右依次计算。
整数连乘乘加乘减混合运算的顺序:先算乘法,再算加法或减法。
教师总结:同学们已经学会了整数的连乘、乘加、乘减混合运算,实际在生活中,不但会遇到整数的计算问题,还会有小数的计算问题,那今天我们就共同找出小数的混合运算规律。这节课我们就来为我们学校图书馆的建设出一份力。
设计理由:运用温故知新的导人方法。学生的学习是由浅入深、循序渐进的过程。通过复习学生原有知识
内容里与新知识相联系的有关内容,提出符合学生知识水平、富有启发性的问题、小测验等形式多样的教学活动作为新旧知识联系的支点,导入新课。
提醒:点这里加小编微信(领取免费资料、获取最新资讯、解决考教师一切疑问!)









