提醒:点这里加小编微信(领取免费资料、获取最新资讯、解决考教师一切疑问!)
20.在1、2、3、4、5、6六个数中,任选三个数组成没有重复数字且大于400的三位数数字的概率是( A )。
A.1/2 B.1/3 C.1/4 D.1/5
21.已知(x+y):y=1:2,(x+1):z=1:3,则x,y,z的值分别是( D )。
A.1/2,2/5,6/5 B.1/5.-2/5,-6/5 C.-1/5,2/5,-6/5 D.-1/5,-2/5,6/5
22.已知,x^2+y^2=5,x+y=1,则X,Y的值 ( A )。
A.X=2,y=1或x=-1,y=2
B.x=-2,y=-1
C.x=2,y=-1或x=1,y=2
D.x=2,y=-1
23.在直角三角形中△ABC中,∠C=90度,sinA=1/2,则cosB=( B )。
A.√3/2 B.1/2 C.√3/4 D.√3/3
24.边长为4cm的正方形外接圆与内切圆的面积只差为( A )cm^2
A.4π B.6π C.8π D.5π
25.不等式组2x+4<0,x+1≥0,接集是( A )。
A.-1≤x<2 B.-1
26.计算-32的结果是( A )。
A.-9 B.9 C. -6 D.6
27.因式分解(x-1)2-9的结果是( D )。
A.(x+8)(x+1) B.(x-2)(x-4)
C.(x-2)(x+4) D.(x+2)(x-4)
28.点A、B、C、E在正方形网格中的位置如图所示,则,sinA=( D )。
A.BE/BC B.AE/AC C.AD/AC D.BD/BC
29.边长为6的正方形外接圆和内切圆的周长之差为( D )cm。
A.5√3π B.4√3π C.6 √3π D.2√3π
30.在△中ABC,DE//BC,若AD:BD=1:3,DE=2,则BC=( A )。
A.8 B. 6 C.4 D.2
31.在半径为R的园中,内接正方形壹外接正六边形的边长之比是( D )。
A.2:3 B.2::3 C.√3::2 D.√2:1
32.若关于X的一元二次方程(k-1)x^2+2x-2=0有两个不相等的实数根。则K的取值范围( C )。
A.K>1/2 B.k≥1/2 C.k>1/2且k≠1 D.k大于等于1/2且k≠1
33.下图中的物体的左视图是( D )。
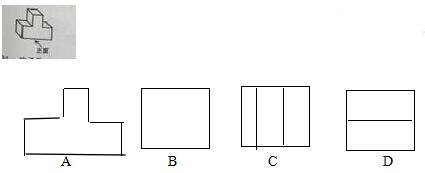
34.一次函数y1=kx+b与y2=x+a的图像如图,则下列结论(k<0;a>0当)x<3,y1
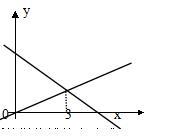
A.0 B.1 C.2 D.3
35.将抛物线y=x^2向下平移1各单位,再向左平一2各单位,所得的新的抛物线的表达式是( D )。
A.y=(x-1) B.y=(x-2)^2+1 C.y=(x+1) ^2-2 D.y=(x+2)^2-1
36.某篮球12名队员的年龄如下图所示:

则这12名队员年龄的众数和中位数分别是( B )。
A.2,19 B.18,19 C.2,19.5 D.18,19.5
37相交两心园的圆心距是5,如果其中一个园的半径是3,那么另一个圆的半径可以是( B )。
A.2 B.5 C.8 D.10
38.关于二次函数y=2+(x+1)^2的图像,下列判段正确的是( D )。
A.函数开口向上 B.图像的对称轴为x=1
C.图像由最高点 D.图像的顶点坐标为(-1.2)
39.当A≠0时,函数y=ax+1与y=a/x在同一坐标系中图像可能是( C )。
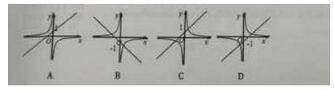
40.在△ABC中,BD平分∠ABC,CD平分∠ACB,∠A=50则∠BDC=( B )。
A.100 B.115 B.120 C.125
42.设{an}是公比为q的等比数列,则“q>1”是{an}为递增数列的( C )。
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
43.设随机变量X服从正态分布N(0.1),P(X>1)=0.2,则P(-1
A.0.1 B.0.3 C.0.6 D.0.8
50.奇函数f(x)(x∈r)满足f(-3)=0,且在区间(0,2)与(2,+∞)上分别是递减和递增,则不等式(1-x^2)f(x)>0的解( D )。
A.(-∞,-3)∪(1.4) B.(-∞,-3)∪(1,∞)
C.(-∞,-3)∪(-1,1)∪(3,∞) D.(-∞,-3)(1,3)
52.点x=0是函数y=x的( B )。
A.驻点但非极值点 B.拐点 C.驻点且是拐点 D.驻点且是极值点
53.曲线y=1/丨x丨的渐近线情况是( D )。
A.只有水平渐近线
B.只有垂直渐近线
C.既有水平渐近线又有水平渐近线
D.即无水平渐近线有无垂直渐近线
54.《义务教育数学课程标准(2011)》明确提出了四个基本目标,分别是基础知识,基础技能基础思想和( C )。
A.基本能力 B.基本习惯 C.基本态度 D.基本经验
55.《义务教育课课程标准(2011)》中提到的培养学生问题解决的能力,涵盖( D ),提出问题,分析问题,解决问题。
A.阅读问题 B.发现问题 C.创新问题 D.辨别问题
56.“综合实践”是一类以( B )为载体,以学生自主参与为主的学习活动。
A.知识 B.探讨活动 C.问题 D.调查
57.通过义务教育阶段的数学学习,学生能了解数学的价值,提高数学的兴趣,增强学好数学的信心。养成良好的学习习惯,具有初步的( C )和科学态度
A.推理能力 B.应用能力 C.创新能力 D.思维能力
58.学习评价的主要目的是为了全面了解学生数学的( C )和结果,激励学生学习和改进教师教学。
A.过程 B.能力 C.目标 D.质量
59.数学课堂教学应该以学生的认知发展水平和已有的经验为基础,面向全体学生,注重( A )。和因材施教。
A.探究性 B.启发式 C.互助性 D.讲授型
60.学生学习应该是一个活动,主动的和富有个性化的过程认真听讲,积极思考、动手实践( B )、合作交流,都是学习数学的重要方式。
A.自主探究 B.独立探究 C.自主思考 D.极创新
提醒:点这里加小编微信(领取免费资料、获取最新资讯、解决考教师一切疑问!)









